CURSO DE ELETRÔNICA - Grandezas CA

Missão do Sistema SENAI

                Contribuir para o fortalecimento da indústria e o desenvolvimento

     pleno e sustentável do País, promovendo a educação para o trabalho  e  a

     cidadania, a assistência técnica e tecnológica, a produção e disseminação

     de informação e a adequação, geração e difusão de tecnologia.

     Nosso negócio

       Educação para o Trabalho e Cidadania. 

   

Relação de fase entre grandezas CA

A relação de fase é uma comparação entre os momentos em que os fenômenos elétricos acontecem. Pode-se, por exemplo, estabelecer uma relação de fase entre duas tensões CA de mesma freqüência. Para isto, escolhe-se um momento como ponto de referência, normalmente o pico do ciclo positivo (ou negativo) de uma das tensões CA, como mostrado na Fig.1.

Fig.1 Ponto de referência da tensão alternada CA₁.

Verifica-se em seguida a outra tensão no circuito neste mesmo momento, conforme mostrado na Fig.2.

Fig.2 Tensão CA₂ no mesmo momento que ocorre o pico na tensão CA₁.

Ao se comparar a segunda tensão CA₂ com a tensão CA₁ de referência, pode ocorrer uma das três situações apresentadas graficamente na Fig.3.

                   

                      

Fig.3 Posições possíveis do pico de tensão do semiciclo positivo de uma tensão CA com respeito a uma tensão de referência.

Na situação (a), o pico positivo da tensão CA₁ coincide com o pico positivo da tensão CA₂ no mesmo instante.

Nesta situação, diz-se que as tensões CA₁ e CA₂ estão em fase.

 Duas tensões CA estão em fase quando seus picos positivos e negativos ocorrem ao mesmo tempo.

Nas outras duas situações (b) e (c), as tensões CA₁ e CA₂ atingem os valores máximos (picos positivos e negativos) em instantes diferentes.

Quando isto ocorre, diz-se que as tensões CA₁ e CA₂ estão defasadas.

 Duas tensões CA estão defasadas quando seus picos (positivos ou negativos) ocorrem em momentos diferentes.

Observando os gráficos em que as tensões CA₁ e CA₂ estão defasadas, verifica-se que estes gráficos apresentam diferenças entre si.

No gráfico da Fig.3b, o ponto de referência da tensão CA₁ (pico positivo), ocorre antes do pico positivo da tensão CA₂. A tensão CA₂ atingirá o pico positivo depois da CA₁. Neste caso, diz-se que a tensão CA₂ está atrasada com relação a CA₁ ou a tensão CA₁ está adiantada com relação a CA₂.

No gráfico da Fig.3c, a tensão CA₁ atingirá o pico positivo depois da CA₂. Neste caso, diz-se que a tensão CA₂ está adiantada em relação a tensão CA₁ ou a tensão CA₁ está atrasada em relação a tensão CA₂.

Ângulo de defasagem entre grandezas CA

O adiantamento ou atraso de uma tensão CA em relação a outra é dado em graus (º). Um ciclo completo de uma CA corresponde a 360º, como mostrado na Fig.4.

Fig.4 Ciclo completo de uma CA.

Por conseqüência, como mostrado na Fig.5, tem-se que: um semiciclo de uma CA tem 180º, meio semiciclo de uma CA tem 90º e um quarto de semiciclo de uma CA tem 45º.

  

                  

Fig.5 Subdivisões de um ciclo de uma CA.

Com base nesta divisão do eixo horizontal, pode-se determinar de quantos graus é a defasagem entre uma tensão CA e a outra.

As Figs. 6, 7, 8 mostram exemplos de tensões CA defasadas.

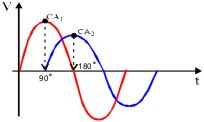
pico positivo de CA₁ :  90º

pico positivo de CA₂ : 180º

defasagem                 : 180º - 90º = 90º

 Fig.6 CA₂ está atrasada 90º com relação a CA₁.

pico positivo de CA₁ : 135º

pico positivo de CA₂ :  90º

defasagem                : 135º - 90º= 45º

 Fig.7 CA₁ está atrasada 45º em relação a CA₂.

pico positivo de CA₁ :  60º

pico positivo de CA₂ : 200º

defasagem                : 140º

Fig. 8 CA₂ está atrasada 140º em relação a CA₁.

Existe ainda um caso particular de defasagem, como mostrado na Fig.9.

pico positivo de CA₁ :  90º

pico positivo de CA₂ : 270º

defasagem                 : 180º

 Fig. 9  CA₁ e CA₂ em oposição de fase

Neste caso, diz-se apenas que CA₁ está em oposição de fase com CA₂ ou que CA₁ e CA₂ estão em anti-fase.

Vetores

Existem grandezas que podem ser expressas simplesmente por um número e uma unidade. Por exemplo, quando se diz que a temperatura em um determinado momento é de 20º C, a informação que se quer dar é perfeitamente compreensível. Este tipo de grandeza é chamada de grandeza escalar. Alguns exemplos de grandezas escalares são: o tempo, a distância e a massa.

Para algumas grandezas, entretanto, um número e uma unidade não são suficientes.

Suponha a seguinte atuação: em meio a uma guerra, um general envia a seguinte mensagem ao comandante da tropa que está no fronte de batalha: “desloque o seu regimento 6km do ponto atual o mais breve possível”.

O comandante certamente ficará em situação difícil, pois a mensagem não diz se o deslocamento deve ser para o norte, sul, leste oeste ou mesmo para direções intermediárias.

Pelo exemplo, conclui-se que para definir um deslocamento não é suficiente dizer apenas de quanto este deve ser.

Grandezas como o deslocamento são denominadas de grandezas vetoriais. Outros exemplos de grandezas vetoriais são: a força, a velocidade e o campo elétrico.

Para a perfeita determinação de uma grandeza vetorial são necessárias três informações:

·        Um valor numérico, denominado de módulo.

·        Uma direção.

·        Um sentido.

Assim, o comandante não teria tido dúvidas se a mensagem do general fosse: “Desloque o seu regimento 6km do ponto atual, na direção norte - sul, sentido do sul o mais breve possível”.

Uma grandeza vetorial pode ser representada graficamente através de um segmento de reta orientada denominado de vetor.

A Fig. 10 mostra alguns vetores.

Fig.10 Vetores.

Como se pode observar, em qualquer um dos vetores da Fig.10, esta representação gráfica fornece as três informações necessárias a respeito da grandeza vetorial.

A Fig.11 mostra um vetor e sua reta suporte com a indicação de seu módulo, sua direção e seu sentido.

Fig.11 Módulo, direção e sentido de um vetor.

Os vetores constituem-se em fator de simplificação na análise de situações diárias.

Supondo-se, por exemplo, que alguém deseje levar uma mesinha com a televisão do canto esquerdo da sala para o canto direito e está pensando em como fazê-lo, como ilustrado na Fig.12. Intuitivamente, qualquer pessoa sabe que terá que empurrar ou puxar a mesinha com uma determinada força para que isto aconteça.

Fig.12 Deslocamento de uma mesa.

Esta força pode ser representada através do vetor da Fig.13.

·        Módulo: valor numérico da força para movimentar a mesinha.

·        Direção: horizontal.

·        Sentido: da esquerda para direita.

Fig.13 Vetor força.

RESULTANTE DE UM SISTEMA DE VETORES

Em muitas situações existe mais de uma força atuando sobre o mesmo ponto ao mesmo tempo. Nestes casos, empregar uma representação gráfica simplifica a determinação de uma solução.

Suponha, por exemplo, que uma pessoa precise puxar a caixa pesada ilustrada na Fig.14. Ao tentar, esta pessoa conclui que sozinha não consegue movimentar a caixa.

Fig.14 Deslocamento de uma caixa pesada.

A solução é pedir ajuda, incluindo mais uma força no sistema. Naturalmente esta segunda força tem que atuar na mesma direção e sentido e no mesmo ponto de aplicação que a primeira para que o resultado (resultante) seja o desejado.

A resultante, neste caso, será a soma das duas forças, atuando na mesma direção e sentido das forças individuais.

A Fig.15 mostra a representação completa do sistema de forças e sua resultante.

Fig.15 Sistema de forças e sua resultante.

Então, pode-se afirmar que se duas forças F₁ e F₂ aplicadas no mesmo ponto e atuando tem na mesma direção e mesmo sentido, o vetor resultante tem as seguinte características:

·        Módulo: F₁+F₂.

·        Direção: a da reta que contém as duas forças.

·        Sentido: o mesmo das forças.

Exemplo 1:

Duas pessoas puxam, na mesma direção e sentido uma corda presa a uma carga. A primeira exerce uma força de 45N e a segunda uma força de 55N. Qual o módulo, a direção e o sentido da força resultante?

Observação: Newton (N) é a uma unidade de medida de força.

Solução:

Desenhando-se o diagrama vetorial, tem-se que:

Módulo do vetor resultante: F_R = 45N + 55N = 100N

Direção do vetor resultante: a mesma das forças aplicadas (horizontal).

Sentido do vetor resultante: o mesmo das forças aplicadas (direita para esquerda).

Em algumas situações, as forças de um sistema têm a mesma direção, mas sentidos opostos.

Imagine, por exemplo, a brincadeira de “cabo de guerra” mostrada na Fig.16.

Fig.16 “Cabo de guerra”.

Este é um exemplo típico de sistema onde as forças atuam na mesma direção (a da corda ) e em sentidos opostos.

Considerando a corda como ponto de aplicação das forças, o sistema pode ser representado conforme a Fig.17.

Fig.17 Diagrama vetorial do “cabo de guerra”.

A resultante neste caso, será o resultado da subtração de uma força da outra, com a direção mantida (a da corda) e o sentido da força maior, como mostrado na Fig.18.

Fig.18 Forças em direções opostas.

Se duas forças F₁ e F₂ aplicadas ao mesmo ponto atuam na mesma direção e em sentidos opostos, têm-se para a resultante que:

Módulo: F₁ - F₂ (a maior menos a menor).

Direção: a da reta que contém as duas forças.

Sentido: o da força maior.

Exemplo 2:

Determinar a resultante do sistema de forças da figura abaixo.

Primeiro, verifica-se que F₁ e F₂ atuam na mesma direção e sentido, podendo ser substituídas por uma resultante parcial FR₁.

Da mesma forma pode ser feito com F₃, F₄ e F₅, substituindo por uma resultante parcial FR₂.

 

 Agora é possível determinar a resultante do sistema FR como sendo :

         FR = 110N-95N = 15N.

Direção = a da corda (horizontal).

Sentido = o da maior força (para a esquerda).

Existe ainda uma terceira situação em que forças aplicadas no mesmo ponto não têm a mesma direção.

Supondo-se, por exemplo, dois rebocadores puxando um transatlântico através de dois cabos, conforme mostrado na Fig.19.

Fig.19 Transatlântico puxado por dois cabos.

O ponto de aplicação das forças é o mesmo (o transatlântico), porém as direções são diferentes, como pode ser visto na Fig. 20.

Fig. 20 Ângulo entre as forças produzidas pelos rebocadores.

Neste caso a forma mais simples de encontrar a solução é a forma gráfica pela Regra do Paralelogramo.

Deve-se colocar em um papel os dois vetores, desenhados em escala com o ângulo correto entre eles, como mostrado na Fig.21.

Fig.21 Diagrama vetorial da situação mostrada na Fig.19.

Então, traça-se pela extremidade de cada um dos vetores dados uma linha tracejada, paralela ao outro, como mostrado na Fig.22.

Fig.22 Aplicação da regra do paralelogramo.

Forma-se assim um paralelogramo cuja diagonal é a resultante, conforme ilustrado na Fig.23.

Fig.23 Formação gráfica da resultante.

Medindo-se a resultante com a mesma escala usada para os vetores componentes, tem-se o módulo da resultante.

A direção e o sentido ficam estabelecidos automaticamente no traçado gráfico.

Um caso particular desta situação é quando há um ângulo de 90º entre as forças. A Fig.24 mostra esta situação.

Fig.24 Aplicação de duas forças que formam um ângulo de 90°.

A resolução gráfica da Fig.24 mostra que o paralelogramo formado é um retângulo onde a resultante é diagonal, como mostrado na Fig.25.

Fig.25 Força resultante.

Trocando-se um dos vetores de posição, forma-se um triângulo retângulo em que F₁ e F₂ são os catetos e R é a hipotenusa, como mostrado na Fig.26.

Fig.26 Triângulo retângulo tendo a hipotenusa como resultante.

Neste caso, o módulo dos vetores se relacionam segundo o teorema de Pitágoras:

                                     R² = F₁² + F₂²                                                          (1)

 Se duas forças F₁ e F₂  aplicadas ao mesmo ponto formam um ângulo de 90º entre si, a resultante é dada pelo teorema de Pitágoras, ou seja:          .

O ângulo formado entre os vetores componentes e o resultante é dado pelas relações trigonométricas.

                                                                                                                       

Exemplo 3:

Dois rebocadores de 15.000N cada um traciona um transatlântico. Sabendo-se que o ângulo entre os cabos dos dois é de 90º, determinar o módulo da resultante e o ângulo desta com relação ao rebocador.

Solução:

O transatlântico se deslocará em uma trajetória que forma um ângulo de 45º com o cabo do rebocador 1.

Fasores

A análise do comportamento e dos parâmetros de um circuito em CA apresenta certas dificuldades porque os valores de tensão e corrente estão em constante modificação.

Mesmo os gráficos senoidais, que podem ser utilizados com este objetivo, tornam-se complexos quando há várias tensões ou correntes envolvidas com defasagem entre si.

Por este motivo é muito comum empregar gráficos fasoriais em substituição aos senoidais.

Do mesmo modo que o comprimento de um segmento de reta, a sua direção e a sua orientação no espaço representam uma série de grandezas físicas, chamadas então de grandezas vetoriais, existe também uma forma de representar graficamente as grandezas tensão e corrente elétrica senoidais.

Por exemplo, a tensão alternada

                                     V(t) = V_m cos (wt + f)                                           (4)

de amplitude V_m, frequência angular w (rads/s) e fase f (rad ou graus) pode ser representada no plano cartesiano como mostrado na Fig. 27.

Fig. 27 Representação fasorial de uma tensão alternada.

O estudo dos números complexos nos revela que esta é a representação do  número   

 , que na teoria dos circuitos elétricos recebe o nome especial de fasor.

Note que na representação fasorial da tensão senoidal V(t) = V_m cos (wt + f), apenas a amplitude da tensão V_m e o ângulo de fase f são especificados, devendo então a frequência angular ser fornecida a parte.

A representação fasorial de uma tensão ou corrente alternada é muito útil, pois nos possibilita visualizar o comportamento relativo dessas grandezas.

Nos gráficos fasoriais, um segmento de reta pode ser usado para representar a tensão ou corrente eficaz correspondente a uma CA senoidal. A Fig.28 ilustra este princípio.

Fig.28 Representação fasorial de uma onda senoidal.

O sistema de gráficos fasoriais permite a representação de qualquer número de tensões com quaisquer defasagens. O ângulo de defasagem entre as tensões CA é representado graficamente por um ângulo entre os fasores.

REPRESENTAÇÃO FASORIAL DE GRANDEZAS SENOIDAIS EM FASE

Quando duas CA estão em fase, pode-se dizer que o ângulo de defasagem entre elas é 0º. A Fig.29 mostra um exemplo.

Fig.29 Exemplo de duas tensões alternadas em fase.

Esta situação pode ser representada fasorialmente, considerando-se três aspectos:

·        Um segmento de reta representa o valor eficaz de CA₁.

·        Outro segmento de reta representa o valor eficaz de CA₂.

·        O ângulo entre os dois fasores representa o ângulo de defasagem, que neste caso é de 0º.

A Fig.30 mostra o gráfico senoidal e vetorial de duas CA em fase.

Fig.30 Gráfico senoidal e fasorial de duas tensões alternadas em fase.

REPRESENTAÇÃO FASORIAL DE GRANDEZAS SENOIDAIS DEFASADAS

Para representar grandezas senoidais defasadas, os princípios são os mesmos:

·        Um segmento de reta para cada grandeza.

·        Um ângulo entre os fasores que expressa a defasagem.

Há porém alguns cuidados a serem observados. Sempre que se observa um gráfico de grandezas senoidais defasadas toma-se uma das grandezas como referência para depois verificar se as outras estão adiantadas ou atrasadas em relação a estas.

Para os gráficos fasoriais obedece-se o mesmo princípio. Em geral, costuma-se traçar um sistema de eixos ortogonais que servirá de base para o gráfico e traçar o fasor de referência no sentido horizontal para a direita, como mostrado na Fig.31.

Fig.31 Traçado do fasor de referência.

Veja, por exemplo, o gráfico senoidal apresentado na Fig.32 com a CA₁ tomada como referência.

Fig.32 Tensões senoidais CA₁ (referência) e CA₂.

A partir do fasor de referência, posiciona-se os demais fasores. Fasores colocados no sentido horário estão atrasados com relação a referência e vice versa, como mostrado na Fig.33.

Fig.33 Fasores atrasados e adiantados.

No gráfico senoidal usado como exemplo, a CA₂ está atrasada 90º com relação a CA₁, de forma que o gráfico se apresenta conforme a Fig.34.

Fig.34 Vetor atrasado 90^o .

A seguir estão colocados alguns exemplos de gráficos senoidais e seus respectivos gráficos vetoriais. Os valores apresentados nos gráficos senoidais são valores eficazes.